DTMF的matlab实现

$$ \begin{align*} \newcommand{\dif}{\mathop{}\!\mathrm{d}} \newcommand{\belowarrow}[1]{\mathop{#1}\limits_{\uparrow}} \newcommand{\bd}{\boldsymbol} \newcommand{\L}{\mathscr{L}} \end{align*} $$

实验目的

了解电话按键音形成的原理，理解DTMF音频产生软件和DTMF解码算法；
利用FFT算法识别按键音。

实验要求

设计音频产生函数，音频信号见下图，每个数据信号持续半秒；
实现解码函数：接收（1）产生的DTMF信号，识别信号的频率，并生成包含拨号数字的序列。

实验过程

什么是DTMF？DTMF(Dual Tone Multi Frequency)，双音多频，由高频群和低频群组成，高低频群各包含4个频率。一个高频信号和一个低频信号叠加组成一个组合信号，代表一个数字。高频、低频及对应的数字如下图所示：

频率	1209Hz	1336Hz	1477Hz	1633Hz
697Hz	1	2	3	A
770Hz	4	5	6	B
852Hz	7	8	9	C
941Hz	*	0	#	D

CCITT规定每秒最多按10个键，即每个键时隙最短为100MS，其中音频实际持续时间至少为45MS，不大于55MS，时隙的其他时间内保持静默，因此按键产生双音频信号时，相继的两个信号间隔一段时间；解码器利用这个时间识别出双音频信号，并转换成对应的数字信息，而且要识别出间隙信息。因此流程包含音频任务和静默任务，前者是产生双音频采样值，后者产生静默样值，每个任务结束时，要重置定时器和下一个任务。其中静默任务还要加上一个任务：从数字缓冲区取出数字并解包。

function compound =dtmfDial(numString, Fs)
% DTMF Dial: generate a sound according to the numString 
% numString: the telephone numbers
% Fs: sampling rate

    fl=[697 770 852 941];%低频频率
    fh=[1209 1336 1477 1633];%高频频率

    last_time=0.5;%单个按键声音持续时间
    compound=[];

    for i=1:length(numString)
        switch numString(i)
            case'1'
                freq_low=fl(1);freq_hgh=fh(1);
            case'2'
                freq_low=fl(1);freq_hgh=fh(2);
            case'3'
                freq_low=fl(1);freq_hgh=fh(3);
            case'4'
                freq_low=fl(2);freq_hgh=fh(1);
            case'5'
                freq_low=fl(2);freq_hgh=fh(2);
            case'6'
                freq_low=fl(2);freq_hgh=fh(3);
            case'7'
                freq_low=fl(3);freq_hgh=fh(1);
            case'8'
                freq_low=fl(3);freq_hgh=fh(2);
            case'9'
                freq_low=fl(3);freq_hgh=fh(3);
            case'*'
                freq_low=fl(4);freq_hgh=fh(1);
            case'0'
                freq_low=fl(4);freq_hgh=fh(2);
            case'#'
                freq_low=fl(4);freq_hgh=fh(3);
            case'A'
                freq_low=fl(1);freq_hgh=fh(4);
            case'a'
                freq_low=fl(1);freq_hgh=fh(4);
            case'B'
                freq_low=fl(2);freq_hgh=fh(4);
            case'b'
                freq_low=fl(2);freq_hgh=fh(4);
            case'C'
                freq_low=fl(3);freq_hgh=fh(4);
            case'c'
                freq_low=fl(3);freq_hgh=fh(4);
            case'D'
                freq_low=fl(4);freq_hgh=fh(4);
            case'd'
                freq_low=fl(4);freq_hgh=fh(4);
            otherwise
                error('The n!');
        end
        single=0.25*sin(2*pi*freq_low*[1/Fs:1/Fs:last_time])+... %低频
            0.25*sin(2*pi*freq_hgh*[1/Fs:1/Fs:last_time]); %高频
        single=[single,zeros(1,0.3*Fs)]; %加上间隔
        compound=[compound,single];%将每个按键串在一起
    end
end

numString='123456789*0#';
Fs=8000;
compound = dtmfDial(numString, Fs);
plot(compound);
sound(compound,Fs);%播放声音
%audiowrite('test.wav',compound,Fs);%保存声音文件

产生的音频的时域图如下图所示：

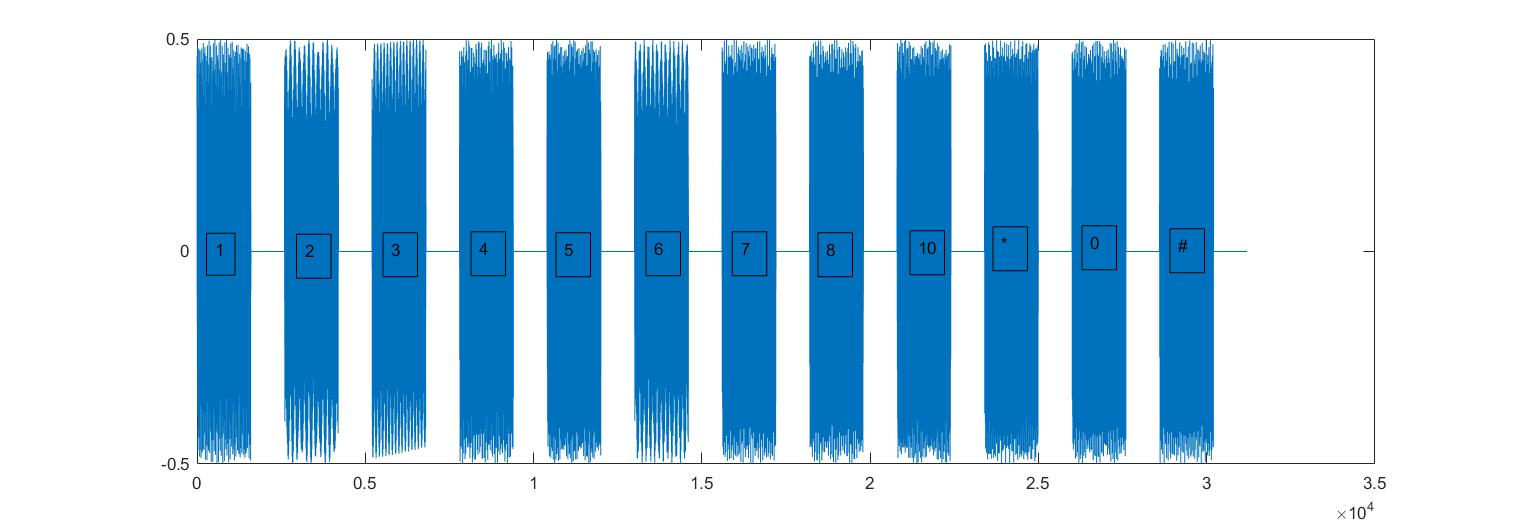
DTMF时域图

为了检测每个数据，我们需要将音频切片。若音频中一段时间内的平均幅度过小，则可认为是静默。因此，我们需要对整个音频进行滑动平均滤波，即：

$$ y(n)=\frac{1}{windowSize}\big[ x(n)+x(n-1)+\cdots+x(n-(windowSize-1)) \big] $$

窗口不能取太大，也不能取太小，否则会导致滤波效果不好。由于最小静默时间为 45ms，所以窗口可以取 5ms. 可以用 filter() 函数进行滤波

function [nstart, nstop]=dtmfCut(compound, Fs)
%return the start and end index of each number
%nstarts: a vector of the start index
%nends: a vector of the end index

    compound = compound(:)'/max(abs(compound)); %归一化
    len = length(compound);
    windowSize = round(0.01*Fs);
    setpoint = 0.02 %低于 2% 的点视为静默
    compound = filter(ones(1,windowSize)/windowSize, 1, abs(compound)); %滑动平均滤波

    compound = diff(compound>setpoint); %差分
    jmp = find(compound~=0)'; %找出跳变点

    if compound(jmp(1))<0 %第1个跳变点为负，说明信号开始时是拨号音
        jmp=[1 jmp];  
    end
    if compound(jmp(end))>0 %最后跳变点为正，说明信号结束时是拨号音
        jmp=[jmp len];
    end 

    index=[];

    while length(jmp>1)
        if jmp(2)>(jmp(1)+10*windowSize) %若两个跳变点时间太短则忽略
            index = [index; jmp(1:2)];
        end
        jmp(1:2)=[];
    end
    nstart = index(1,:);
    nstop = index(2,:);

end

经过上面的处理后，可以得到每个片段的起始点与终止点，如下图所示：

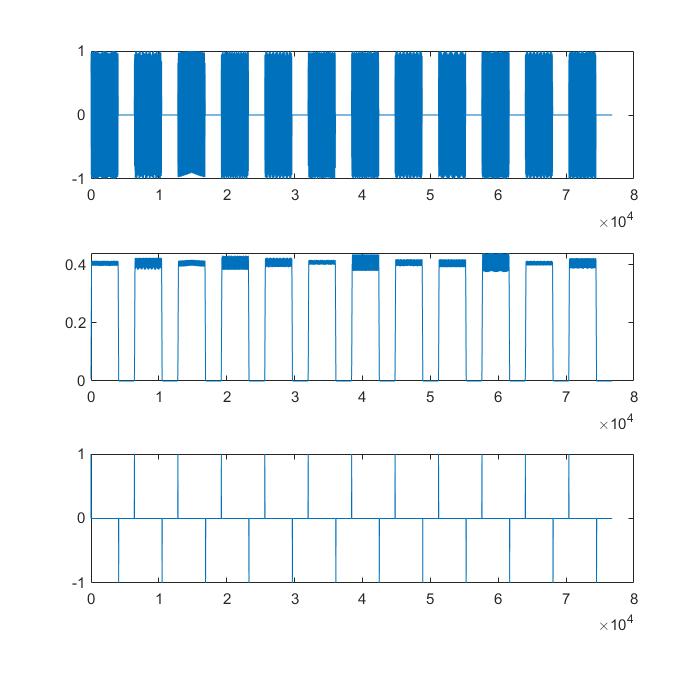
dtmf处理

然后对每个片段进行 DFT 变换，找出峰值。这里我们以第 1 个片段为例子。

for kk=1:length(nstart)
    indx=[nstart(kk):nstop(kk)];
    x_seg(kk,[1:length(indx)])=compound(indx);
end

x_fft = abs(fft(x_seg(1,:)));
[pks, locs]=findpeaks(x_fft,'MINPEAKHEIGHT',max(x_fft)/4);
f=[1:length(x_fft)];
plot(f, x_fft, f(locs), pks, 'or')

得到的 DFT 和峰值如下图所示。

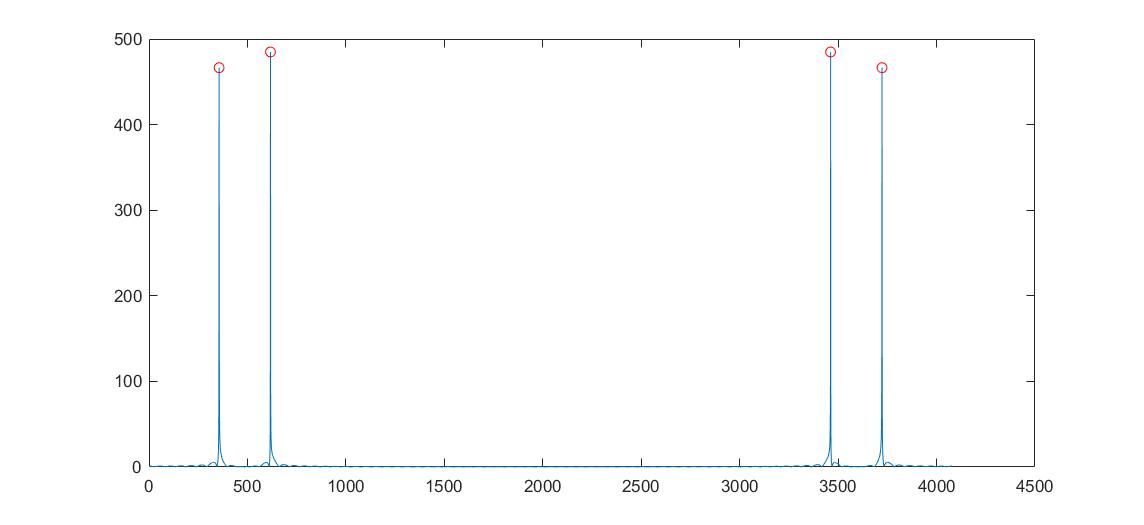
找出峰值后，即可根据下面的公式求出频率：

$$ \Omega_k = 2 \cdot \frac{k}{N} \cdot f_s\\ 其中，k<\frac{N}{2} $$

fk=locs/length(x_fft)*Fs

求出频率为 698.6 和 1210.7。CCITT 规定频率偏移在 1.5% 内为正常，因此可以认为这两个频率近似于 697 和 1209，从而识别出该片段代表 “1”

将上面过程用函数实现，如下。

function numString = dtmfRun(compound, Fs)

    fl=[697 770 852 941];%低频频率
    fh=[1209 1336 1477 1633];%高频频率
    num=['1','2','3','A';
         '4','5','6','B';
         '7','8','9','C';
         '*','0','#','D'];
    
    [nstart, nstop]=dtmfCut(compound, Fs); %获取每个片段的开始与结束位置
    for kk=1:length(nstart) %获取每个片段
        indx=[nstart(kk):nstop(kk)];
        x_seg(kk,[1:length(indx)])=compound(indx);
    end

    x_freq=[];

    for kk=1:length(nstart) %寻峰
        x_fft=abs(fft(x_seg(kk,:)));
        [~, locs]=findpeaks(x_fft,'MINPEAKHEIGHT',max(x_fft)/4);
        fk=locs/length(x_fft)*Fs;
        x_freq=[x_freq;fk(1:2)];
    end

    numString=[];

    for kk=1:length(nstart) %频率转数字
        lnum=0;hum=0;
        f1=x_freq(kk,1);
        f2=x_freq(kk,2);
        lnum=find(abs(fl-f1)./fl<0.015);
        hnum=find(abs(fh-f2)./fh<0.015);
        if lnum~=0 && hnum~=0
            numString=[numString,num(lnum,hnum)];
        end
    end
end

最后验证一下代码的正确性：

numString='123456789*0#';
Fs=8000;
compound = dtmfDial(numString, Fs);
dtmfRun(compound, Fs)

输出：

ans =

    '123456789*0#'

结果正确。

参考

课堂作业