数据链路层
数据链路层的功能
数据链路层的功能:提供有效、可靠的帧传输,具体来说就是:
- 使用物理层提供的服务周期通信信道上发送和接受比特(有效)
- 为网络层提供一个定义良好的服务接口(有效)
- 处理传输错误(可靠)
- 流量控制:调节数据流,确保慢速的接收方不会被快速的发送方淹没(可靠)
打个比方,数据链路层就像旅行社,它已经知道了旅客名单(待发送的数据),现在它要确定这些旅客是做大巴去呢,还是做飞机去,以及路上堵车了怎么办等等。
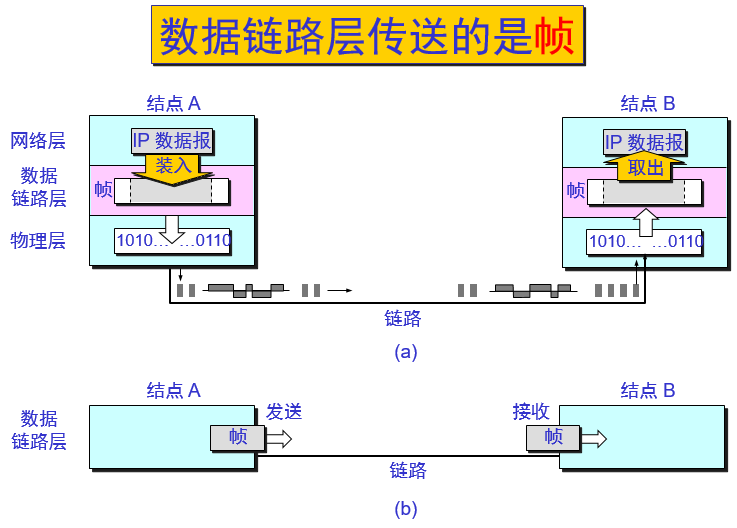
链路层从网络层获取数据后,会将数据封装成 帧(frame),每个帧包括:
- 帧头
- 有效载荷(数据和纠错码)
- 帧尾
数据链路层为网络层提供三种服务:
- 无确认的无连接服务
- 适合误码率低,或对实时性要求高
- 有确认的无连接服务
- 用于时延大且不可靠的链路
- 有确认的面向连接服务
- 用于长距离且不可靠的链路
确认 指接收方受到数据帧后,向发送发发回一个确认。连接 指发送方与接收方在传输数据之前必须建立逻辑连接,传输结束后必须释放连接。
成帧
将原始的位流分散到离散的帧中,叫成帧,成帧的方法有:
- 字符计数法
- 带字节填充的标志字节法
- 比特填充的比特标志法
- 物理层编码违例法
字符计数法
发送方:在每个帧头的第一个字段,标识该帧的长度(包括第一个字段)
接收方:通过第一个字段判断帧在哪里结束
特点:简单,但一旦出错,无法恢复,因为我们无法确定出错的位置(改进方法:带字节填充的标志字节法)
带字节填充的标志字节法
发送方:用特殊字节(Flag)标记帧的开始与结束,如果帧内有 “Flag”,就在前面加上一个转义字符,比如:
- 原始数据:A Flag B
- 传输数据 Flag A ESC Flag B Flag
如果帧内有 “ESC”,也是在前面加上一个转义字符:
- 原始数据:A ESC B
- 传输数据 Flag A ESC ESC B Flag
如果既有 Flag 也有 ESC,或者有多个 Flag 或多个 ESC,则每个前面都要加上一个转义字符:
- 原始数据:A ESC Flag B
- 传输数据 Flag A ESC ESC ESC Flag B Flag
接收方收到一个 ESC,就会删掉它,然后保留后一个字符
特点:
- 按字节来传输,也就是传输的帧的比特数必须是 8 的整倍数(改进方法:比特标志法)
比特标志法
发送方:用一串特殊的比特(01111110)标记帧的开始(用下一个帧的开始来标记结束),如果数据中出现了连续的 5 个 1,就在第 5 个 1 后面插入一个 0,接收方会删除 5 个 1 后面的 0
特点:可传输任意比特数的帧,且传输效率更高
如果某个帧中有 100 个 01111110(Flag),如果用字节填充,那么传输效率只有 50%,如果用比特标志法,那么传输效率有 88.9%
物理层编码违例法
4B/5B码:将 4 个比特映射到 5 个比特中,占用 16 个5B码,剩下的 5B 码可用作帧界(或其他特殊字符)
曼彻斯特编码:从高到低电平跳变表示 1,从低到高电平跳变表示 0,那么可以用从高到高或从低到低作为帧界
特点:使用冗余信号作为帧界,不会出现在数据中,传输效率较高
差错控制
一些概念:
传输错误可分为:单个错误(分散)与突发错误(集中)
检错:检查传输错误
纠错:恢复传输错误
码字:包含数据位与校验位的n位单元
海明距离:两个码字之间不同位的数目(也就是异或后1的个数)。海明距离的意义在于:如果海明距离为 d,则一个码字至少需要发生 d 个错误才能变成另一个码字。
海明距离与检错:海明距离为 d+1 的编码能检测出 d 位差错
海明距离与纠错:海明距离为 2d+1 的编码可以纠正 d 位差错
要理解上面两句话,关键是理解什么叫”海明距离为 d+1 的编码“。加入检错/纠错码后,有些码字是合法的,有些码字是非法的,两个合法码字的最小距离就是这个编码的海明距离。比如说,现在合法码字是{00, 11},那么海明距离是 2,可以检查出 {01,10} 错误,也就是 1 位错误。
检错
奇偶校验:在数据后面增加奇偶校验位,奇校验要求添加校验位后,码字中的 1 的个数为奇数,偶校验则要求为偶数。奇偶校验只能判断出奇数个错误,检错概率为 50%
互联网校验和:
发送端:待校验的相邻字节成对组成16比特的整数 一行,按列从低位开始计算其模2和;并将结果 按位取反码,作为校验和取值。
接收端:检查校验和时,将所有字节,包括校验和, 进行相加并求二进制反码。接收方:如果结果 为全1,无错误
详情请看:Internet 校验和的数学性质
注意:如果某列的模2和有溢出,向高位进位,如果高位产生进位,循环向低位进位。
循环冗余检错码,cyclic redundancy checks, CRC:将 $m$ 位的数据看作是 $m-1$ 次的多项式:$M(x)=x^{m-1}+\cdots+x^0$,并设定一个 $r$ 次生成多项式 $G(x)=x^r+\cdots+x^0$,在 $k$ 位帧后面补上 $r$ 位的校验位得到 $k$ 位的码字,使得码字对应的多项式可被 $G(x)$ 整除。接收方用相同的生成多项式除码字,能整除就说明传输无错误。
要得到校验位,可以采用如 下方法:先将 $M(x)$ 乘以 $x^r$ ,然后模2除1以 $G(x)$,余数就是校验位。把余数补到 $M(x)$ 的后面(等效于减去余数),就能得到码字。下面给出一个例子:
数据为 1101011011,9次多项式
除数为 10011,4次生成多项式
余数计算方法如下:
1100001010
----------------
10011 | 11010110110000
10011
--------------
10011
10011
-------------
00001
00000
------------
00010
00000
-----------
00101
00000
----------
01011
00000
---------
10110
10011
--------
01010
00000
-------
10100
10011
------
01110
00000
-----
1110👈余数
码字:11010110111110国际上常用的生成多项式有:
- CRC-12:$x^{12}+x^{11}+x^3+x^2+x^0$ (用于字符长度6位)
- CRC-16:$x^{16}+x^{15}+x^2+x^0$ (用于字符长度8位)
- CRC-CCITT:$x^{16}+x^{12}+x^{5}+x^0$ (用于字符长度8位)
纠错
只讲一种纠错方法:海明码,在讲之前,先思考一道题目:传输 $m$ 位数据,需要 $r$ 位冗余位,纠正 1 位错误。问 $r$ 与 $m$ 的关系?
假设编码后码字有 $n=m+r$ 位,合法码字有 $2^m$ 个,每个合法码字跳变 1 位后不会变成另一个合法码字,跳变得到的 $n$ 个码字不能用于其他码字,也就是说,总共需要 $(1+n)2^m$ 个码字,于是有:
$$ \begin{cases} (1+n)2^m\leq 2^n\\ n=m+r \end{cases}\\ \Rightarrow (1+m+r) 2^m \leq 2^{m+r}\\ \Rightarrow (1+m+r) \leq 2^r $$我们可以列出如下的表格:
| 冗余 $r$ | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| 最多数据 $m$ | 0 | 0 | 1 | 4 | 11 | 26 |
| 码字 $n$ | 0 | 0 | 3 | 7 | 15 | 31 |
海明码规定,最左边的为第 1 位,并且在 $2^{r-1}$ 的位置放第 $r$ 个校验位($r$ 从 1 开始),其它位放数据,那么我们有:
| 第x位 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 校验位 | # | # | # | # |
对比上面两个表格,我们发现下表这种放置方式符合上表的规定,也就是可以纠错。
进一步规定:校验位是码字中某几个位的偶校验或奇校验。哪些具体是哪些位呢?对于码字中的第 x 位,将 x 展开成二进制的形式,如果二进制从右数起的第 r 位是 1,那么这个码字就被第 r 个校验位校验。
| 第x位(#为校验位) | #0001 | #0010 | 0011 | #0100 | 0101 | 0110 | 0111 | #1000 | 1001 |
|---|---|---|---|---|---|---|---|---|---|
| 第 1 位校验位 | X | X | X | X | X | ||||
| 第 2 位校验位 | X | X | X | X | |||||
| 第 3 位校验位 | x | x | x | x | |||||
| 第 4 位校验位 | x | x |
在接收方,由于第 r 个校验位代表的是二进制第 r 位,那么,如果第 r 个校验位出错,就在第 r 位置 1。最终得到的二进制就是出错的位。(另一种表述方法是:第 r 个校验位出错,就加上 $2^r$,最终得数就是出错位)
海明码只能纠正单个错误,要检查突发错误,我们可以改变发送方式:假如有 k 个码元,排列成一列,然后我们按列发送数据,这样只要突发错误小于等于 k,就能检查出来。
基本数据链路协议
假设:
- 物理层、数据链路层、网络层是独立的进程
- 机器 A 向 机器 B 发送一个面向连接的长数据流
- 机器不会崩溃
为了用代码描述协议,我们在头文件中定义以下数据类型和函数:
#define MAX_PKT 1024 //packet size in bytes
typeof enum {false, true} boolean; //boolean type
typeof unsigned int seq_nr //sequence or ack numbers
typeof struct {unsigned char data[MAX_PKT];} packet; //packet definition
typeof enum {data, ack, nak} frame_kind; //frame_kind definition
typeof struct{ //frames are transported in this layer
frame_kind kind; //what kind of frame
seq_nr seq; //sequence number
seq_nr ack; //acknowledgement number
packet info; //network layer packet
} frame;
void wait_for_event(event_type *event);
void from_network_layer(packet *p);
void to_network_layer(packet *p);
void from_physical_layer(frame *r);
void to_physical_layer(frame *s);
void start_timer(seq_nr k); //重传计时器
void stop_timer(seq_nr k);
void start_ack_timer(void); //捎带确认计时器
void stop_ack_timer(void);
void enable_network_layer(void);
void disable_network_layer(void);
#define inc(k) if(k<MAX_SEO) k=k+1; else k=0;下面先从简到繁介绍三种单工协议(半单工协议):
- 无限制的单工协议
- 单工-停等协议
- 有噪声信道的单工协议
然后我们再扩展到双工
无限制的单工协议
这种协议有几个假设:
- 数据单向传送
- 收发双方的网络层都处于就绪状态
- 处理时间忽略不计(瞬间完成)
- 可用缓存空间无限大
- 信道无噪声(不丢失帧)
这样发方发一个,收方就收一个。用代码表示就是:
typedef enum {frame_arrival} event_type;
#include "protocol.h"
void sender1(void)
{
frame s;
packet buffer;
while(true){
from_network_layer(&buffer); //从网络层拿包
s.info = buffer; //将包放入帧
to_physical_layer(&s); //传帧给物理层,发送帧
}
}
void receiver1(void){
frame r;
event_type event;
while(true){
wait_for_event(&event); //等待帧到达
from_physical_layer(&r); //从物理层取帧
to_network_layer(&r.info); //传包给网络层
}
}单工-停等协议
我们逐步去除单工协议中的假设。由于缓存不可能无限大,接收方可能来不及接收数据,所以发方要等等收方。收方收到帧后,要回传一个哑帧,收方收到哑帧后才传下一个数据。
下面的代码只增加的发送与接受哑帧这两行。
typedef enum {frame_arrival} event_type;
#include "protocol.h"
void sender2(void)
{
frame s;
packet buffer;
event_type event;
while(true){
from_network_layer(&buffer); //从网络层拿包
s.info = buffer; //将包放入帧
to_physical_layer(&s); //传帧给物理层,发送帧
wait_for_event(&event); //等待接收方的确认帧
}
}
void receiver2(void){
frame r,s;
event_type event;
while(true){
wait_for_event(&event); //等待帧到达
from_physical_layer(&r); //从物理层取帧
to_network_layer(&r.info); //传包给网络层
to_physical_layer(&s); //发送确认帧
}
}有噪声信道的单工协议
我们进一步取消“信道无噪声”这个假设,这样收方可能发现帧出错(通过校验位)。我们要求收方要发一个确认帧给发方,发方才会发下一个帧。如果没收到确认帧,那么就重发当前帧。
但帧、确认帧都可能在传输的过程中丢失。为了避免发方无限等待,我们给发方设置一个定时器,如果定时器超时,那么无论有没有收到确认帧,都重传当前帧。
我们将上面的技术称为 肯定确认重传(PAR,Positive Acknowledgement with Retransmission),或 自动重传请求(Automatic Repeat reQuest)。顺带一提,有肯定当然就有否定:否定确认重传(NAR)
但这样又有一个新问题。如果确认帧丢失,那么尽管收方收到了帧,但发方还是会重发,导致收方收到两个重复的帧(又或者说定时器太短,还没收到确认帧就重传了)。为了解决这个问题,我们给每个帧一个序列号。这样收方就能判断前后两帧是否相同。收方发送确认帧时也要用相同的序列号,这样发方才知道哪个帧已经收到了,哪个帧还没收到。
这里有个小细节:由于我们只需要区分前、后帧,所以序号只需要 0,1 即可。发方每次收到确认帧后序号加1模2,收方同理(对应代码中的 s.ack = 1-frame_expected)。
typedef enum {frame_arrival} event_type;
#include "protocol.h"
void sender3(void)
{
seq_nr next_frame_to_send;
frame s;
packet buffer;
event_type event;
next_frame_to_send = 0;
from_network_layer(&buffer); //从网络层拿包
while(true){
s.info = buffer; //将包放入帧
s.seq = next_frame_to_send; //帧序列号
to_physical_layer(&s); //传帧给物理层,发送帧
start_timer(s.seq); //开始计时
wait_for_event(&event); //等待接收方的确认
if(event == frame_arrival){
from_physical_layer(&s);
if(s.ack == next_frame_to_send){ //获得确认
stop_timer(s.ack); //停止计时器
from_network_layer(&buffer);
inc(next_frame_to_send); //加1模2
}
}
}
}
void receiver3(void){
seq_nr frame_expected;
frame r,s;
event_type event;
frame_expected = 0;
while(true){
wait_for_event(&event); //等待帧到达
from_physical_layer(&r); //从物理层取帧
if(event == frame_arrival){
from_physical_layer(&r);
if(r.seq == frame_expected){
to_network_layer(&r.info); //传包给网络层
inc(frame_expected);
}
}
s.ack = 1-frame_expected;
to_physical_layer(&s); //发送确认帧
}
}滑动窗口协议
注意到确认帧中是没有数据包的,我们可以把确认帧放到数据帧中,称为 捎带确认。如果确认帧很久都没等到一个数据帧(又用一个计时器),那就发空的确认帧。
另外为了提高信道利用率,我们在等待确认帧时也可以继续发送数据,这样就会一次发送若干个数据,这种技术称为 批量数据 或 管道化技术,每一批数据称为一个 窗口 的数据,发完后窗口滑动到下一批数据,因此这类协议统称为 滑动窗口协议。
在滑动窗口数据中,发方有一个 发送窗口(已发送未确认),收方有一个 接收窗口(待接收)。
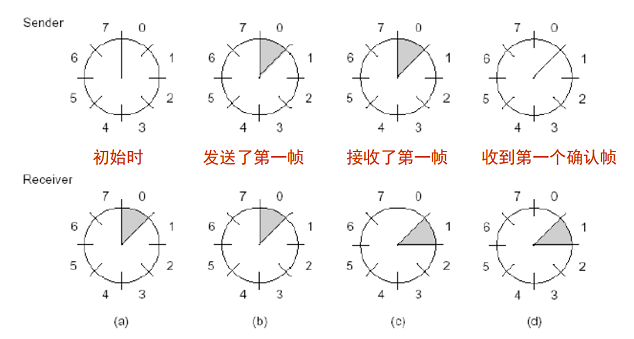
滑动窗口协议的工作顺序如下(窗口大小是 0):
- 初始时,接收窗口在 0 的位置
- 发方发送第 0 帧后,发送窗口在 0 的位置
- 收方收到了序列号为 0 的帧,接收窗口滑动到 1,并回发确认
- 发方收到序列号为 0 的确认,于是发送下一帧,发送窗口滑动到 1.
由于这是双工协议,所以我们不再区分 sender 和 receiver
void protocol4(void){
seq_nr next_frame_to_send;
seq_nr frame_expected;
frame r,s;
packet buffer;
event_type event;
next_frame_to_send = 0; //第一帧要传0号帧
frame_expected = 0; //接收方期望接受的是对方的0号帧
from_network_layer(&buffer);
s.info = next_frame_to_send;
s.ack = 1-frame_expected;
to_physical_layer(&s);
start_timer(s.seq);
while(true){
wait_for_event(&event){
if(event == frame_arrivel){
from_physical_layer(&r);
if(r.seq == frame_expected){ //是不是期望的帧
to_network_layer(&r.info);
inc(frmae_expected); //移动接收窗口
}
if(r.ack==net_frame_to_send){ //是不是确认了
stop_timer(r.ack);
from_network_layer(&buffer);
inc(next_frame_to_send); //移动发送窗口
}
s.info = buffer;
s.seq = next_frame_to_send;
s.ack = 1-frame_expected; //捎带确认
to_physical_layer(&s);
start_timer(s.seq);
}
}
}
}注意:我们的滑动长度为 1,所以 seq 和 ack 都是 0/1 交替出现。下面我们来分析上述代码的工作情况。
| 情况 | 分析图 |
|---|---|
| 正常工作 | 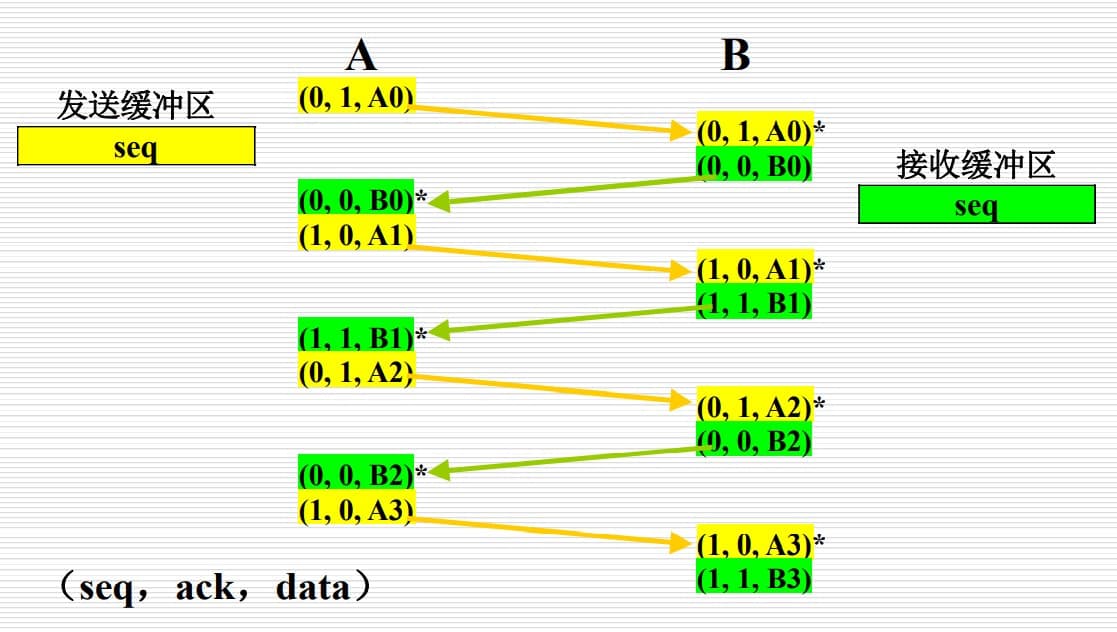 |
| 未收到确认(会浪费带宽) | 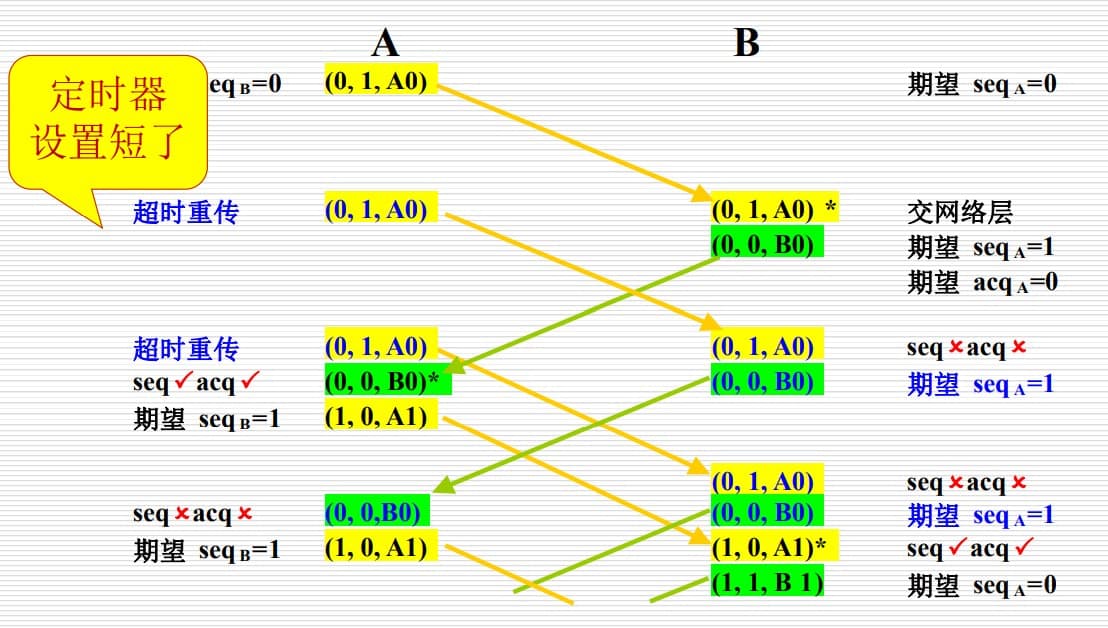 |
| 同时开始传输(会浪费带宽) | 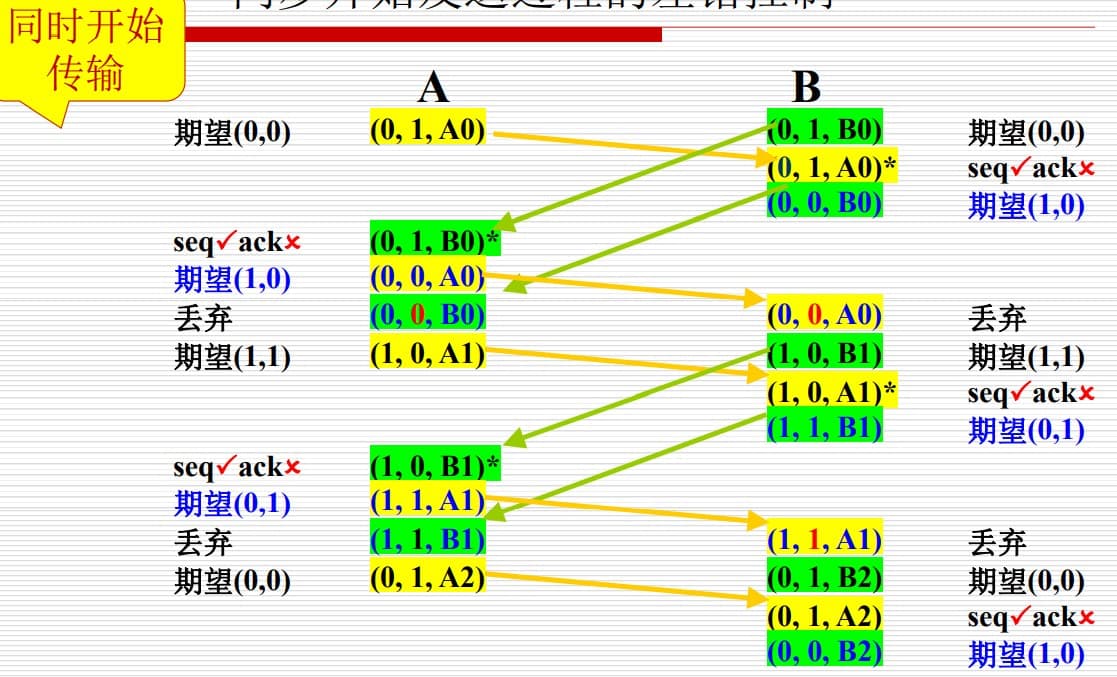 |
假如忽略处理帧的时间,并忽略确认帧的长度,并假设信道的传输速率是 $b$ bps,每帧的大小是 $k$ bps,来回时间是 $R$ sec,那么:
- 发方发送数据帧需要 $k/b$ sec
- 帧传到收方需要 $R/2$
- 收方发送的确认帧到达发方需要 $R/2$
总的传输时间是 $k/b+R$,而发送有效数据的时间是 $k/b$,那么利用率为 $\frac{k/b}{k/b+R}=\frac{k}{k+bR}$。由于 $R$ 一般远大于 $k/b$,所以利用率非常低。
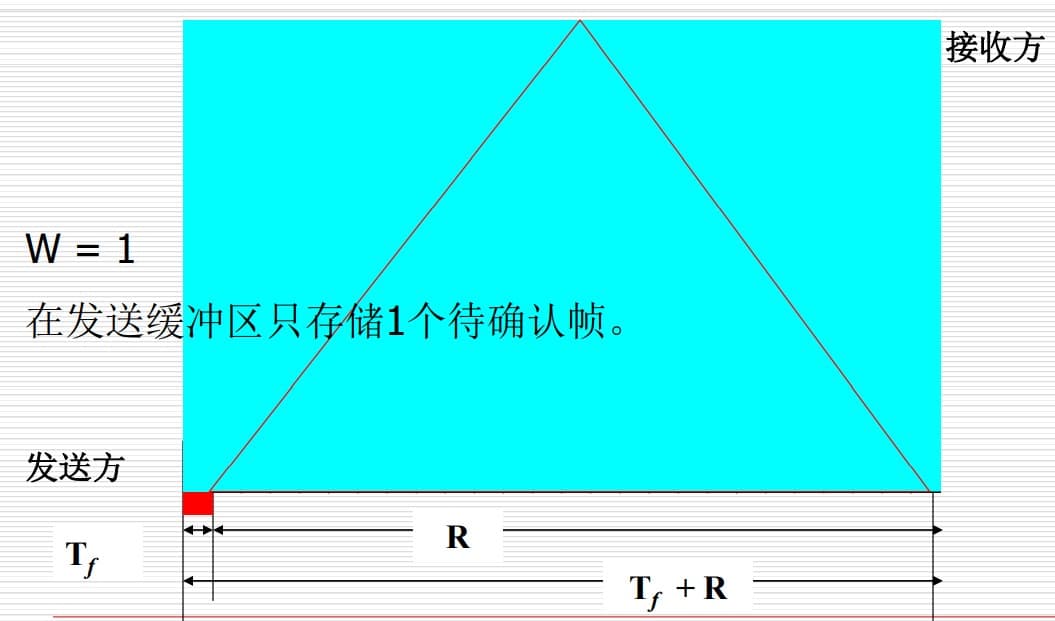
为了提高利用率,我们可以考虑增大 $k$(也只能增大 $k$,因为 $b,K$ 是固定的),也就是增大窗口大小,使得一次发多帧。
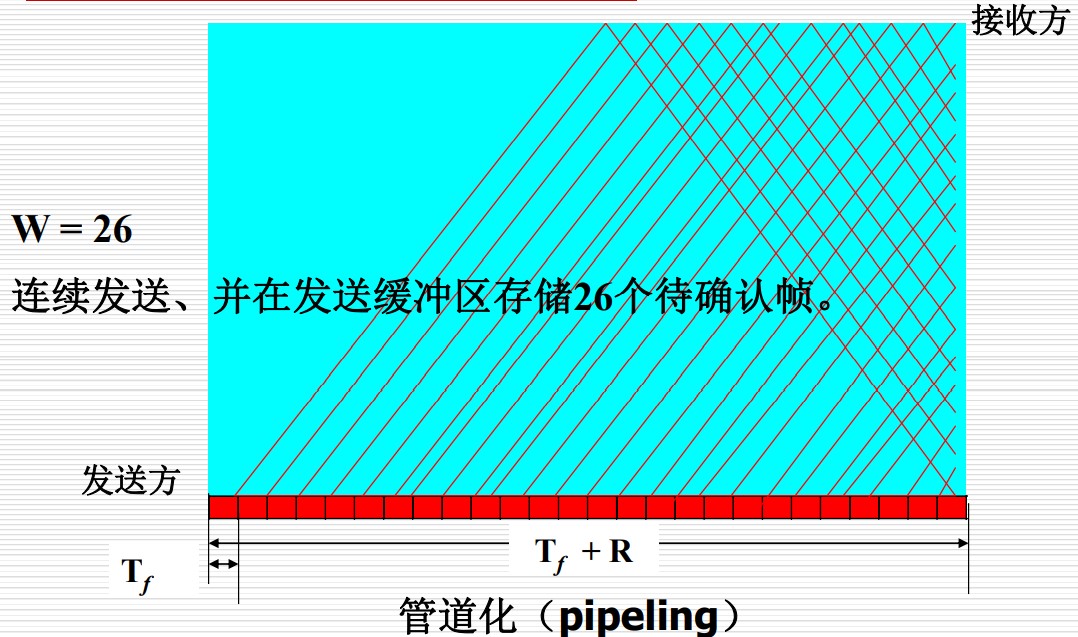
假设窗口大小是 $W$,那么利用率为 $\dfrac{Wk/b}{k/b+R}=\dfrac{Wk}{k+bR}$,由于利用率不大于 1,所以有 $W\leq 1+bR/k$。
也可以感性的角度去计算 $W$。从我们定义一帧从发送到接收期间可容纳的帧的 数量 为 带宽-延迟积 $BD=b\cdot\dfrac{R}{2}/k$,则从第一帧发送到第一个确认帧到达期间可容纳的窗口值为 $W \leq 2\cdot BD+1$
管道化技术会引入新的问题:连续发送W个数据帧,其中有一帧出错,但其后续帧被成功发送。这时候有两种策略:
- 丢弃错帧和后续帧:回退n帧协议
- 丢弃错帧:选择重传协议
回退n帧协议
接收方的接收策略选择:丢弃错帧,其后续帧因不是期望接收帧也被丢弃(接收窗口为1)。
发送方的重传策略选择:缓存在发送窗口中的出错帧以及其后续帧全部重发。
选择重传协议
数据链路协议实例
PPP
模2运算:模2加减(就是异或):0+0=0。0+1=1,0-1=1,0-0=0;模2除:列竖式计算时,使用模2减的除法 ↩︎