数据库总结

March 16, 2020·

数据库，从删库到跑路。

书写规范

定义与定理的格式如下：
【定义】数据库：……
【定理】数据库定理：……
若需要在下面写注释，则用引用的形式：
注：……
列表一律用有序表，而不是无序表，并且每一项若有标题，则标题粗体
凡是有一定”步骤“的解题方法，均使用类 Python 写：
【方法】：
```
if …… #如果
while …… #循环……
```

第一章数据和数据管理

基本概念

【定义】数据：一切能被计算机存储和梳理，反应客观实体信息的物理符号，是信息的载体

【定义】信息：有一定含义、经加工过、对决策有价值的数据。特点：

可感知
可理解
可传递
可存储

数据与信息的联系：
数据是信息的载体，信息是数据的内涵；
同一信息有不同数据表现形式，同一数据也有不同解释

【定义】数据处理：将数据转换成信息的过程。分类：

集中处理：数据存储和处理由一台计算机完成
分散处理：数据分块存储在多台计算机上，它们之间没有联系，处理由单台计算机完成
分布处理：数据分块存储在多台计算机上，可以和其他计算机一起处理

其他分类方式：

联机/脱机
批处理/分时/实时
单道/多道/交互式

数据管理技术的发展

【定义】数据管理：对数据的组织、编目、定位、存储、检索和维护等

数据管理是数据处理的基本环节
数据管理是数据库系统研究内容的核心

人工管理阶段：磁带/汇编/批处理
1. 特点：
  1. 数据不保存在计算机中
  2. 没有专用的软件对数据进行管理
  3. 以应用为中心，数据面向应用
文件系统阶段：磁盘/高级语言/操作系统
1. 优点：
  1. 数据可长期保存在磁盘上
  2. 有专用的软件对数据进行管理
  3. 数据与程序具有一定的独立性
  4. 文件组织多样化
2. 缺点：
  1. 文件内部的数据没有结构化
  2. 文件间缺乏联系导致数据冗余
  3. 仍以应用为中心，数据面向应用，数据共享程度低
数据库系统阶段：：网络及大容量磁盘/关系数据库的理论基础

【定义】数据冗余：在一个以上的位置不必要地产生重复数据。导致后果：数据不一致；数据异常

【定义】数据库：一般指相互关联的数据集合

【定义】数据库管理系统 DBMS：指帮助用户创建和管理数据库的应用程序集合

数据库系统的特点：

支持数据的多视图，数据冗余度降低
有较高的数据独立性
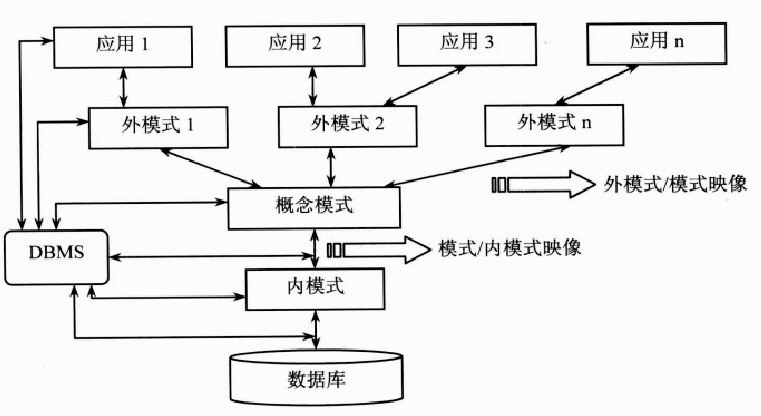
1. 三级结构：用户的逻辑结构；数据库的整体逻辑结构；数据库的物理结构
2. 两级映射：模式/内模式映射；外模式/模式映射
3. 两个独立性：物理独立性；逻辑独立性
数据库系统向用户提供高级的接口
查询的处理和优化
数据的备份与恢复
数据的安全性
并发控制
数据的完整性(integrity)约束
1. 正确性：如年龄属于数值型数据
2. 有效性：指数据是否在其定义的有效范围
3. 相容性“指表示同一事实的两个数据应相同

数据模型

数据模型的重要性：

数据模型是设计者、程序员、终端用户三者沟通的桥梁
数据模型是数据库的框架

数据描述的三个层次：

现实世界
信息世界
1. 【定义】 实体(entity) 客观存在可以相互区别的事物。
2. 【定义】 属性(attribute) 实体所具有的特征。
3. 【定义】 实体型(Entity Type) 若干个属性型组成的集合可以表示一个实体的类型，简称实体型。
4. 【定义】实体集(Entity Set) 具有相同性质的同类实体的集合。
5. 【定义】实体标识符(identifier) 能惟一标识每个实体的属性或属性集。
机器世界
1. 【定义】记录(record) 数据项的有序集合。
2. 【定义】字段(Entity Set) 对应于属性的数据
3. 【定义】文件(file) 同一类记录的汇集
4. 【定义】关键字(key) 与实体标识符相对应。
5. 【定义】域(domain) 属性值的取值范围。

数据联系：

联系（Relationship）：
1. 实体内部的联系通常是指组成实体的各属性之间的联系；反映在数据上是一个记录内各数据项间的联系；
2. 实体之间的联系通常是指不同实体集之间的联系；反映在数据上是记录与记录之间的联系。
实体间的联系
1. 一对一联系(one-to-one relationship)
2. 一对多联系(one-to-many relationship)
3. 多对多联系(many-to-many relationship)

结构数据模型由数据结构、数据操作、数据约束三部分组成。

为了描述以上各种实体、属性、联系，引入关系模型：

基本概念：

【定义】关系一个关系对应一张二维表。
【定义】元组表格中的一行。
【定义】分量元组中的一个属性值
【定义】关系模式 对关系的描述，一般表示为：关系名（属性 1，属性 2，……属性 n）。

数据操纵：查询；插入；删除；修改

完整性约束：

实体完整性
参照完整性
用户定义的完整性

优点：

有较强的数学理论基础
结构无关性
改进的概念简单性
支持非过程化的数据库语言
更容易的数据库设计、实现、管理和使用
强大的关系数据库管理系统

缺点：

大量的硬件与软件系统开销
可能助长拙劣的设计和实现
可能助长“信息孤岛”问题

为了解决上述缺点，引入实体联系模型(entity relationship model)

第二章数据库系统概论

模式

【定义】模式（schema）：是数据库的抽象描述。（数据模型是其主体）主要描述内容：数据项的名称、数据项的数据类型、约束、文件之间的相互联系等。

模式图：使用图表显示的模式。源模式：用语言书写的模式。目标模式：把源模式翻译成机器代码，变为计算机可使用的模式。模式演化：模式根据需求进行改变。

三级模式结构:

目的：实现程序－数据独立性
分级：
1. 外模式可称用户视图。每个外模式可以描述某个特定的用户所使用的那一部份数据库。
2. 概念模式简称为模式，是全局数据视图的描述。模式处于三级结构的中间层，它是数据库的整体数据，又称用户共同视图。
3. 内模式在内部级上，用于描述数据库的存取路径和数据存储的全部细节。（硬件）
优点：
1. 保证数据的独立性。将模式和内模式分开，保证了数据的物理独立性；将外模式和模式分开，保证了数据的逻辑独立性。
2. 简化了用户接口
3. 有利于数据共享，减少了数据冗余
4. 有利于数据的安全保密

四种数据记录格式：（PPT123 页）

物理记录 = 一个块（约 256-4096 字节）
内部记录 = 实际的数据记录 + 表示数据结构的相关指针和标志
概念记录 = 学生的基本数据 + 学籍 + 户籍 + 病历
外部记录

两级映射：

目的：在内部实现三个抽象层次（三级模式）的联系与转换
分级：
1. 对于每一个外模式，都存在一个外模式/模式映射,它确定了数据的局部逻辑结构与全局逻辑结构之间的对应关系。
2. 外模式可有多个，而概念模式、内模式只能各有一个。所以模式 /内模式映射是唯一的, 它确定了数据的全局逻辑结构与存储结构之间的对应关系。

两级数据独立性：

数据的逻辑独立性是指当数据的总体逻辑结构改变时，数据的局部逻辑结构不变。由于应用程序是依据数据的局部逻辑结构编写的，所以应用程序不须修改，从而保证了数据与程序间的逻辑独立性。
数据的物理独立性是指当数据的存储结构改变时，数据的逻辑结构不变，所以应用程序也不必改变，从而保证了数据与程序间的物理独立性。

数据库管理系统

【定义】数据库管理系统：指帮助用户创建和管理数据库的应用程序集合。用户在数据库系统中的一切操作，包括定义、构造、操纵等，都是通过 DBMS 进行的。

数据库系统

数据库（Data Base，DB)是按一定结构组织并长期存储在计算机内的、可共享的大量数据的有机集合。其实就是存放数据的仓库，只不过这些数据存在一定的关联、并按一定的格式存放在计算机上。例如，把一个学校的学生、课程、学生成绩等数据有序的组织并存放在计算机内，就可以构成一个数据库。
数据库管理系统（Data Base Management System，DBMS）是管理和维护数据库的系统软件。常用的 DBMS 有：Oracle、DB2、SqlServer、MySql 等
数据库管理员（Date Base Administrator ,DBA)管理操作数据库人员。
数据库系统（Data Base System，DBS）是实现有组织的、动态地存储大量关联数据、方便多用户访问的计算机软件、硬件和数据资源组成的系统，简化为：DBS=计算机系统（硬件、软件平台、人）+DBMS+DB

第三章关系模型（重要）

只有了解关系数据库理论，才能设计出合理的数据库。在一个不合法的数据模型上盲目地开发应用系统，不但费时费力，即使做出来，维护也很困难。

关系

【定义】关系：A relation is a table with columns and rows

【定义】属性：Attribute is a named column of a relation.

【定义】域：一组相同数据类型的值的集合

【定义】元组：Tuple is a row of a relation.

【定义】度或目：Degree is a number of attributes in a relation.

【定义】基数：Cardinality is a number of tuples in a relation.

【定义】关系数据库：Relational Database is a collection of normalized relations.

【定义】笛卡尔积：一组域的乘积，即 $D_1 \times D_2 \times \cdots D_n = \\{ (d_1, d_2, \cdots, d_n) \vert d_i \in D_i, i = 1, 2, \cdots, n \\}$

关系的数学定义：一般地，关系可以定义为笛卡尔积 D1× D2× …×Dn 的子集，称在域 D1, D2, …, Dn 上的关系，表示为 R(D1, D2, …, Dn) 其中：R 为关系名； n 为关系的度或目(degree)。关系是笛卡尔积上的有限子集

关系与笛卡尔积的区别：笛卡尔积不满足交换律，关系满足交换律

关系的键：

超键(Super Key) ：若关系中的某一属性组的值能唯一地标识一个元组，则称该属性组为超键
候选键(Candidate Key) ：若关系中的某一超键，当去掉其中任一属性后，均不再能为超键，则称其为候选键。关系模式中的所有属性的组合是这个关系模式的候选键，称为全键(All-key)
主键(Primary Key)：若一个关系有多个候选键，则选其中一个为主键。主键的诸属性称为主属性(Prime attribute)。不包含在任何候选键中的属性称为非键属性(Non-key attribute)。
外键(Foreign Key) ：若关系 R 的某个属性组合 A 不是 R 的候选键，却是另一个关系 S 的候选键，则称 A 为 R 的外键。关系 R 和 S 不一定是不同的关系。基本关系 R 为参照关系（Referencing Relation），基本关系 S 为被参照关系（Referenced Relation）或目标关系（Target Relation）

关系的性质：

属性值的原子性
属性的同质性同一属性名下的各属性值必须来自同一个域，是同一类型的数据。
属性的顺序无关性在定义一个关系模式时，交换属性的先后顺序不会改变关系的实际意义。
不同属性的异名性
元组的唯一性（许多关系数据库产品没有遵循这一性质）
元组的顺序无关性

关系模式

关系模式是型，是对关系的描述

关系模式可形式化地表示为：$R(U, D, dom, F)$

R 关系名
U 组成该关系的属性名集合
D 属性组 U 中属性所来自的域
dom 属性向域的映射集合
F 属性间的数据依赖关系集合

关系模式通常可以简记为：$R(U)$ 或 $R(A_1, A_2, …, A_n)$

$R$ 关系名
$A_1, A_2, …, A_n$ 属性名

关系模式与关系：

关系模式 :对关系的描述；静态的，稳定的
关系：关系模式在某一时刻的状态或内容；动态的、随时间不断变化的

ER 图转换为关系模式的原则：

对 ER 图中的每个“实体集”，都应转换成一个关系，该关系内至少要包含对应实体的全部属性。
对 ER 图中的每个“联系”，要根据实体联系的方式，采取不同的方法加以处理，有的需把“联系”自身用一个关系来表示，有的则把“联系”纳入表示实体的关系中。
将每个强实体类型 E，转换成一个包含 E 的所有简单属性的关系 R。对于复合属性，则只包括其简单成员属性。选择一个实体标识符作为 R 的主键。
将每个属主实体类型 E 的弱实体类型 W 创建关系 R，并把 W 的所简单属性（或复合属性的简单成员属性）作为 R 的属性。除此之外，R 的主键是 E 的主键和 W 的部分键的组合。
对于 1:1 的二元联系 R，参与该联系的实体为 S 和 T。把 R 的属性放到任一实体（如 S）中，并把 T 的主键作为 S 的外键。
若实体间联系是 1:N，则在 N 端实体类型转换成的关系模式中加入 1 端实体类型的键和联系类型的属性。
若实体间联系是 M:N，则将联系类型也转换成关系模式，其属性为两端实体类型的键加上联系类型的属性，而键为两端实体键的组合。
为每个多值属性 A 创建一个新的关系 R。关系 R 包括一个对应于 A 的属性和外键 K,K 是表示具有属性 A 的实体类型或联系类型的关系的主键属性。R 的主键是 A 和 K 的联合。如果多值属性是复合属性， R 还要包括其简单成员属性。
为每个 n 元联系类型 R 创建一个新的关系 S，其中 n>2。S 的主键是参与联系的实体的所有主键的组合。并把联系的简单属性（或复合属性的简单成员属性）作为 S 的属性。
将超类/子类映射为关系，较常用的方法是：为超类 C 及其属性创建了关系 L，为每个子类 Si 创建关系 Li,每个 Li 专有（或局部）属性和超类 C 的主键，该主键也是每个 Li 的主键。

关系概念模式：由若干个关系模式组成的集合，描述关系数据库中全部数据的整体逻辑结构。
关系外模式：是关系概念模式的一个逻辑子集，描述关系数据库中数据的局部逻辑结构。
关系内模式：是数据文件（包括索引等）的集合，描述数据的物理存储。

关系的完整性（Relational Integrity）：

正确性
有效性
相容性

关系模型的三类完整性约束：

实体完整性：保证一个数据（实体）是可识别的，保证每个元组是可区分的（主键）
参照完整性：数据间的关联和保证关联的正确性（外键）
用户定义的完整性：保证一个数据的取值合理

关系数据语言

关系数据描述语言（DDL）
关系数据操纵语言（DML）
标准数据库语言 SQL

第四章关系运算

记关系$R$的属性为$A_1，A_2，…，A_n$。

记关系$R$的元组为$t$。

假设有同类关系 R 和 S，若 R 中的任何一个元组必然是 S 的一个元组，则称关系 S 包含关系 R，记为$R \subseteq S$ 或 $S \supseteq S$ 。

若同时存在$R \subseteq S$ 和 $S \subseteq R$，则称 R 等于 S，记为 $R=S$。

关系代数

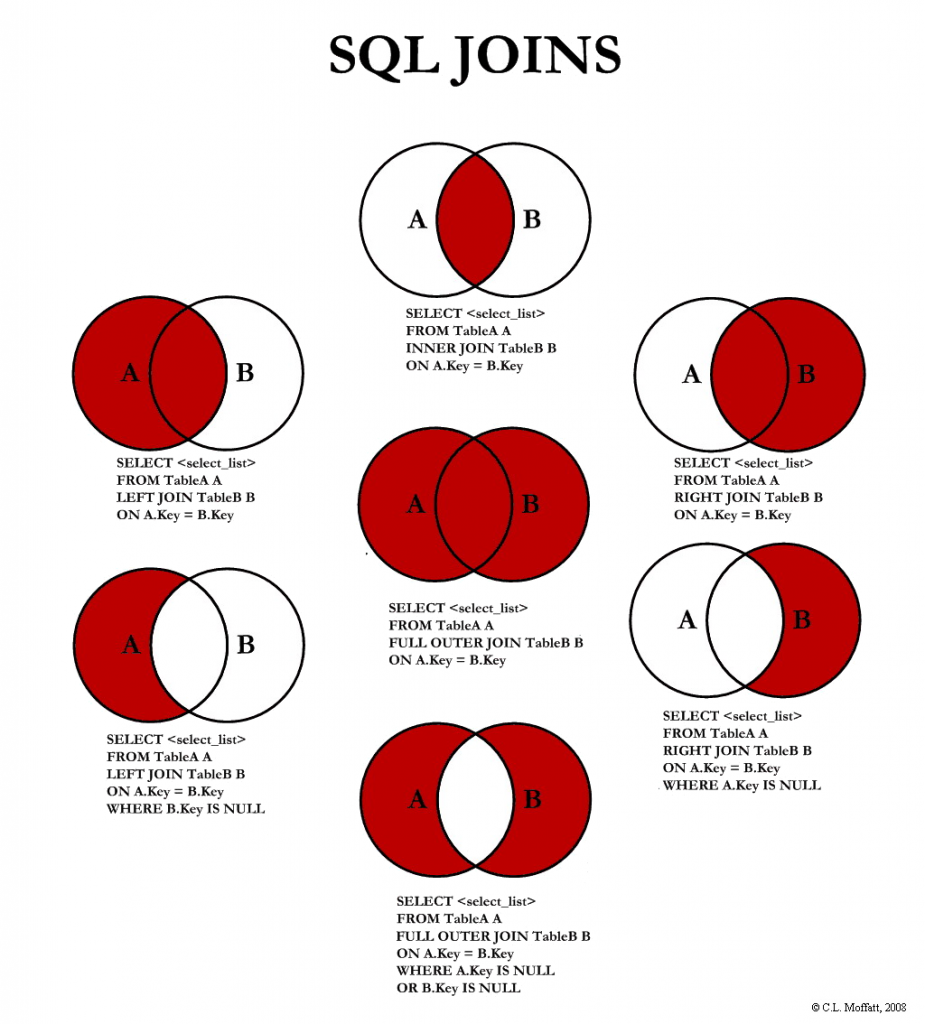
五种基本操作：并；差；乘积；选择；投影

传统的集合操作：并；差；交；乘积

专门的关系操作：选择；投影；连接；自然连接；除法；扩充的关系代数操作

并：$R \cup S \equiv \\{ t \vert t \in R \vee t \in S \\}$
差：$R - S \equiv \\{ t \vert t \in R \wedge t \notin S \\}$
乘积：$R \times S \equiv \\{ t \vert t= \wedge t^r \in R \wedge t^s \in S \\}$
选择：$\sigma_F(R) \equiv \\{ t \vert t \in R \wedge F(t) = \rm{ture} \\}$
投影：$\pi_{i_1, i_2, \cdots, i_m}(R) \equiv \\{ t \vert t = \wedge t^r \in R\\}$
交：$R \cap S \equiv \\{ t \vert t \in R \wedge t \in S \\} = R - (R-S)$
连接：$R \bowtie_{ i \theta j} S \equiv \\{ t \vert t= \wedge t^r \in R \wedge t^s \in S \wedge t_i^r \theta t_j^s\\}$
自然连接（natural join）：$R \bowtie S$ 在 R×S 中，选择 R 和 S 公共属性值均相等的元组，并去掉 R×S 中重复的公共属性列。如果两个关系没有公共属性，则自然连接就转化为笛卡尔积。
除法：：把 S 看作一个块，如果 R 中相同属性集中的元组有相同的块，且除去此块后留下的相应元组均相同，那么可以得到一条元组，所有这些元组的集合就是除法的结果。
外连接：$$R ] \bowtie_{ i \theta j} [ S$$ 如果 R 和 S 自然连接时，把 R 和 S 原来要舍弃的元组都放到新关系中，若对方关系没有相应的元组，新元组中其他的属性应填上空值 NULL。

关系代数表达式的应用

设教学数据库中有 3 个关系模式：

学生关系 S(SNO,SNAME,AGE,SEX)
学习关系 SC(SNO,CNO,GRADE)
课程关系 C(CNO,CNAME,TEACHER)

检索特定列和特定行：
1. 检索课程号为 C2 的学生的学号和成绩：$\pi_\rm{Sno, GRADE} ( \sigma_\rm{CNO = "C2"}(\rm{SC}))$
跨表检索特定列和特定行：
1. 检索学习课程号为 C2 的学生学号与姓名：先查找后自然连接 $\pi_\rm{SNO, SNAME}(\rm{S}) \bowtie \pi_\rm{SNO} (\sigma_\rm{CNO = "C2"} (\rm{SC}))$ ；先自然连接后查找略
2. 检索选修课程名为 MATHS 的学生学号与姓名：先自然连接后查找 $\pi_\rm{SNO, SNAME} (\sigma_\rm{CNAME = "MATHS"}(S \bowtie SC \bowtie C))$
3. 检索所学课程包含 S3 所学课程的学生学号：$\pi_\rm{SNO, CNO}(SC) \div \pi_\rm{CNO}(\sigma_\rm{SNO="S3"}(SC))$
至少/至多：
1. 检索至少选修课程号为 C2 和 C4 的学生学号： $\pi_\rm{SNO}(\sigma_\rm{1=4 \wedge 2="C2" \wedge 5="C4"}(SC \times SC))$
不：
1. 检索不学 C2 课的学生姓名与年龄：$\pi_\rm{SNAME, AGE}(S) - \pi_\rm{SNAME, AGE}(\sigma_\rm{CNO = "C2"}(S \bowtie SC))$
2. 注意区分：查询没有不及格的学号：所有学号-有不及格的学号 √ / 有过及格的学号 ×

查询优化策略：

尽可能早地执行选择及投影操作
把乘积和随后的选择合并成联接操作
一连串的选择和一连串的投影应同时运算
若在表达式中多次出现某个子表达式，应预先将该子表达式算出结果并保存起来，避免重复计算。
在联接前适当地对关系文件进行预处理。如对文件进行排序和建立索引。

元组关系演算

【定义】关系演算：把数理逻辑的谓词演算推广到关系运算中。分为：

元组演算——以元组为变量
域演算——以域为变量

元组表达式 $= \\{ t \vert P(t) \\}$

t 是元组变量，表示一个元数固定的元组，必须是 P(t) 中惟一的自由元组
P(t) 是公式，相当于条件表达式
$\\{ t \vert P(t) \\}$ 是满足 P 的所有元组 t 的集合

原子公式：

R(t)：t 是关系 R 的一个元组
t[i]θC 或 Cθt[i] 表示这样一个命题：“元组 t 的第 i 个分量与 C 之间满足 θ 运算”。
t[i]θu[j] 表示这样一个命题：“元组 t 的第 i 个分量与元组 u 的第 j 个分量之间满足 θ 运算”。

元组变量性质：

存在量词 $\exists$
全称量词 $\forall$
自由变量：如果没有对元组变量使用存在量词 $\exists$ 或全称量词 $\forall$，那么这些元组变量称为自由元组变量
约束变量：若在一个公式中对元组变量使用了存在量词 $\exists$ 或全称量词 $\forall$，则称这些元组变量为约束变量。

元组演算公式（formulas）：元组演算公式的递归定义：

每个原子公式是一个公式
设 P1 和 P2 是公式，那么下列四项也是公式：
1. $\urcorner P1$：对 P1 取反
2. $P1 \vee P2$：若 P1、P2 同时为真，则为 $P1 \vee P2$ 真
3. $P1 \wedge P2$：若 P1、P2 之中有一个为真或两个均为真，则 $P1 \wedge P2$ 为真
4. $P1 \Rightarrow P2$：若 P1 为真同时 P2 为假，则 $P1 \Rightarrow P2$ 为假；否则 $P1 \Rightarrow P2$ 为真
设 P1 是公式，t 是 P1 中的元组变量，那么下列两项也是公式：
1. $(\exists t)(P1)$：若有一个 t 使 P1 为真，则 $(\exists t)(P1)$ 为真
2. $(\forall t)(P1)$：“对所有的 t，使 P1 都为真，则 $(\forall t)(P1)$ 为真
运算符的优先级从高到低依次为：$\theta ; \exists 和 \forall; \urcorner; \wedge和 \vee; \Rightarrow$
所有公式均按上述的规则经有限次复合求得，除此之外构成的都不是公式。

元组关系演算的完备性：

$R \cup S = \\{ t \vert R(t) \vee S(t) \\}$
$R - S = \\{ t\vert R(t) \wedge \urcorner S(t) \\}$
$R \times S = \\{ t \vert (\exists u)(\exists v) \Big( R(u) \wedge S(v) \wedge t[1] = u[1] \wedge t[2] = u[2] \wedge t[3] = u[3] \wedge t[4] = v[1] \wedge t[5] = v[2] \wedge t[6] = v[3] \Big) \\}$
$\sigma_\rm{2="24"}(R) = \\{ t \vert R(t) \wedge t[2] = 24 \\}$
$\pi_\rm{1,3} (R) = \\{ t \vert (\exists u)(R(u) \wedge t[1] = u[1] \wedge t[2] = u[3]) \\}$

域关系演算

域关系演算类似于元组关系演算，不同的是公式中的变量不是元组变量，而是表示元组变量各个分量的域变量。域变量的变化范围是某个值域而不是一个关系。域演算表达式的一般形式为： $\{ t_1 t_1 \cdots t_k \vert P(t_1, t_2, \cdots, t_k) \}$:

$t_i$ 是域变量或常量
P 是 k 元关系
$P(t_1,t_2,…,t_k)$ 表示这样的命题： “以 $t_1,t_2,…,t_k$ 为分量的元组在关系 P 中”。

元组表达式与域表达式的转换：

对每个 k 元的元组变量，引入 k 个域变量 $t_1 t_2 \cdots t_k$
用 $t_1 t_2 \cdots t_k$ 替换元组表达式中的元组变量 $t$ ，用 $t_i$ 替换元组表达式中的元组变量 $t[i]$；
对于每个量词 $(\exists t)$ 或 $(\forall t)$ ，在量词的作用范围内，首先，用 $t_1 t_2 \cdots t_k$ 替换元组表达式中的元组变量 $t$，用 $t_i$ 替换元组表达式中的元组分量 $t[i]$，然后，用 $(\exists t_1)(\exists t_2) \cdots (\exists t_k)$ 替换 $(\exists t)$，用 $(\forall t_1)(\forall t_2) \cdots (\forall t_k)$ 替换 $( \forall t)$。
若能消去某些域变量，则对域表达式进行化简。

第五章关系模式设计

【定义】泛模式：将所有的属性放在一个表中

设计数据库主要的就是设计表的格式，也就是设计关系模式。如果关系模式没设计好，那么可能出现以下问题：

数据冗余
比如学生和课程如果放在一张表存，那么每个学生的姓名就会出现多次
更新异常
还是学生和课程如果放在一张表存，如果只更新了其中一条记录，那么冗余的记录就没有更新到
插入异常
如果学生未选课，那么可能导致学生无法插入
删除异常
如果删除某个学生的记录，而那个学生恰好是某门课的最后一个学生，那么可能会将那门课也一起删除。（虽然听起来没什么毛病，如果把课换成班主任就有毛病了）

为了消除这些问题，需要先理解属性之间的“联系”

函数依赖（Functional Dependency）

定义

【定义】函数依赖：设关系模式$R(U, F)$，$U$ 是属性集，$F$ 是函数依赖集。设 $X, Y$ 是 $U$ 的子集，如果对于 $X$ 的每一个值，$Y$ 都有唯一的值与之对应，则 $X$ 决定 $Y$，或 $Y$ 依赖 $X$，记作 $X \rightarrow Y$，称为模式 $R$ 的一个函数依赖

注：依赖的分类：
完全函数依赖
部分函数依赖
平凡的函数依赖

$$F \vert= X \rightarrow Y$$

【定义】函数依赖的闭包：函数依赖集 $F$ 和所有被它函数蕴涵的函数依赖所组成的集合称为 $F$ 的闭包，记作 $F^+$

【定义】属性集的闭包：设关系模式$R(U, F)$，$U$ 是属性集，$F$ 是函数依赖集。属性集 $X$ 是 $U$ 的子集。用 $F$ 推出所有 $X \rightarrow A$ （$A$ 是属性集），全体 $A$ 的集合称为 $X$ 关于 $A$ 的闭包，记为 $ X^+ $

由上面的定义，我们可以重写候选键的定义：设关系模式$R(U, F)$，$U$ 是属性集，$F$ 是函数依赖集。设 $K$ 是 $U$ 的子集。若 $K \rightarrow U \in F^+$ ，且不存在 $K$ 的子集 $K’$ ，使 $K' \rightarrow U \in F^+$ 成立，则 $K$ 是 $R$ 的一个候选键。

【方法】下面解释求属性集 $X$ 的闭包 $X+$ 的过程（有点类似于 BFS 广度优先搜索）：

#X = [x1, x2, x3 ……]
#最开始时设置一个A和B
A = []
B = X
while A!=B:
    A=B
    for i in F: #F为函数依赖集
        #对于 F 中函数依赖 i：X->Y
        if i.X in B:
            B.append(i.Y)

定理

设关系模式$R(U, F)$，$U$ 是属性集，$F$ 是函数依赖集。设 $W, X, Y, Z$ 是 $U$ 的子集，则有以下定理成立：

【定理】Armstrong 推理规则

自反率：若$Y \subseteq X$，则 $X \rightarrow Y$
增广率：若 $X \rightarrow Y$，则 $XZ \rightarrow YZ$
传递率：若 $X \rightarrow Y, Y \rightarrow Z$，则 $X \rightarrow Z$
*合并率：若 $X \rightarrow Y, X \rightarrow Z$，则 $X \rightarrow YZ$
*伪传递率：若 $X \rightarrow Y, WY \rightarrow Z$，则 $WX \rightarrow Z$
*分解率：若 $X \rightarrow Y, Z \subseteq Y$，则 $X \rightarrow Z$
*伪增高率：若 $X \rightarrow Y, Z \subseteq W$，则 $XW \rightarrow YZ$

最小函数依赖集

【定义】等价（覆盖）：若对于函数依赖 $F, G$，有 $F \subseteq G^+, G \subseteq F^+, F^+ = G^+$，则 $F$ 和 $G$ 等价（覆盖）

【定义】最小函数依赖集：满足以下条件的函数依赖集称为最小函数依赖集 $F_\rm{min}$：

每个函数依赖，其右部均为单个属性；（右边无冗余）
左部不可拆分；（左边无冗余）
删去一个函数依赖后的依赖集不等价于原依赖集；（整个都不冗余）

【方法】下面是求最小函数依赖集的过程：

for i in F:
    #对于 F 中函数依赖 i：X->Y
    F = F-i;
    F = F+seperate(i.Y)#将右边拆成单个

for i in F:
    if F == F-i:
        F = F-i;#检查每个依赖是否冗余

for i in F:
    #删除 i.X 中的部分属性，看 F 是否还等价于原 F
    #是，则删除 i.X 中的冗余部分

分解

无损连接分解（数据完整性）

【定义】无损连接分解：若分解后的关系能通过自然连接得到原关系，则称这种分解为为无损关系分解

【定理】测试定理：对于一分为二的分解，其为无损连接的充要条件是：$R1 \cap R2 \rightarrow (R1 - R2)$ 或 $R1 \cap R2 \rightarrow (R2 - R1)$，即分解后的交集能决定分解后的差集

【方法】判断某个分解是不是无损连接分解：

#第一步：列表，每一列为每个属性，每一行为每一分解关系
#第二步：若对于第 i 行第 j 列，若属性 j 在关系 i 中，则填入“ai”
#第三步：
while 表不可再修改:
    for 每个函数依赖X->Y in 函数依赖集:
        if 有多行的 X 列相同（都是a或都是b）:
            将 Y 列全改为相同（都是a或i最小的b）
if 有一行都为 a:
    为无损分解

保持函数依赖分解（语义完整性）

无损连接分解不一定是保持函数依赖的；保持函数依赖的分解不一定是无损连接的。

如果一个分解能够保持函数依赖集 F，那么在数据操作时，只要每个分解后的关系模式都满足自身的函数依赖约束，就可确保整个数据库中数据的语义完整性不受破坏。

范式

主属性：在关系模式 R 中，若属性 A 是 R 的某候选关键字的一部分，则称 A 为主属性。

非主属性：在关系模式 R 中，除了主属性之外的其他属性。

部分依赖：对于函数依赖$X\rightarrow Y$，如果存在 X 的真子集 X‘，使得 $X' \rightarrow Y$也成立，则称 Y 部分依赖于 X。

完全依赖：对于函数依赖$X\rightarrow Y$，如果 X 的任一真子集 X‘，都有 $X' \nrightarrow Y$，则称 Y 完全依赖于 X。

传递依赖：如果$X\rightarrow Y$，$Y \rightarrow Z$，且 $Y \nrightarrow X$，Z 不是 Y 的子集，则称 Z 传递依赖于 X。

将分解的程度分为：

第一范式（1st Normal Form, 1NF）：最基本的范式，关系中的每个属性都是不可再分的最小数据单位
第二范式：满足 1NF，且非主属性都完全函数依赖于某个候选关键字（候选键）
第三范式：满足 2NF，且非主属性都非传递依赖于某个候选关键字（候选键）
BC 范式（Boyce-Codd Normal Form，BCNF）：满足 1NF，且所有函数依赖 $X \rightarrow Y$ 中的 $X$ 都是超键，即：
1. 所有非主属性对每一个码都是完全函数依赖；
2. 所有的主属性对每一个不包含它的码，也是完全函数依赖；
3. 没有任何属性完全函数依赖于非码的任何一组属性。

【方法】已知关系模式 $R(U, F)$，$U$ 是属性集，$F$ 是函数依赖集。将 $R$ 无损连接和保持函数依赖地分解为第三范式：

#若 F 中只有一个依赖：X->A，且满足 XA=R，则 R 已是第三范式
#对每一个 X->A，都分解成一个关系模式{X, A}
#若有多个 X->A1, X->A2, X->A3，将其合并为一个关系模式{X, A1, A2, A3}
#若分解后，没有一个关系模式包含 R 的所有关键字，则创建一个包含 R 的所有关键字的关系模式
#分解结束

【方法】已知关系模式 $R(U, F)$，$U$ 是属性集，$F$ 是函数依赖集。将 $R$ 分解为 BCNF：

#假设初始的分解 p={R}
#若 p 中的所有关系模式都是 BCNF，则分解结束，否则进行如下分解：
#对于 p 中非 BCNF 的关系模式 S，S 中必包含一个函数依赖 X->A，满足 X 不是 S 的键，且 A 不属于 X。设 S1 = XA，S2=S-A，用 S1,S2 代替 S
#循环上一步骤直到 p 中的所有关系模式都是 BCNF
#分解结束

第六章数据库安全

事物

【定义】事务：一个操作序列，要求满足：

原子性：要么完全执行，要么不执行
一致性：数据结构和数据联系在事务前后保持一致
隔离性：事务不允许被其他事务打断
持久性：事务完成后会对数据库留下永久的痕迹

在 SQL 中，每一条操作语句都是一个事务，称为隐式事务；当然，在 SQL server 中，可以将一段语句定义为事务，称为显示事务：

BEGIN
...
END
commit [事务名]

如果事务中途被外界打断，可以进行：

回滚：回滚到执行事务前
恢复：根据日志文件，执行未执行的语句

对于多个事务，存在两种操作顺序：

串行：一个完成后再做另一个
并发：相互穿插，一个执行时跳到另一个

由于操作系统中的进程是并发运行的，所以多个事务有可能是并发的，会产生一定问题（丢失更新、不一致分析、读脏数据），在此引入并发控制措施：封锁机制，即加入两种锁：

排他锁（eXclusive Lock，X 锁）：不允许其他事务读写，又称为写锁
共享锁（Share Lock，S 锁）：允许其他事务读，又称为读锁

为了定义锁定的时间等规则，需要封锁协议：

一级封锁协议：事务在修改对象前，先加排他锁，直到事务结束；如果仅仅是读取，则不用加锁。
二级封锁协议：在一级封锁协议上，加上：读取对象需要加共享锁，并于读完后解除锁。
三级封锁协议：在二级封锁协议上，加上：读取对象需要加共享锁，并于事务完成后解除锁。

但可能会出现：

死锁
活锁
阻塞

要解决死锁，有两种方法：

悲观：只有当锁的拥有者释放该锁，其他用户才能执行与该锁冲突的操作
乐观：用户读数据时不锁定数据；执行更新时查看另一用户读过数据后是否更改了数据，如果是，将回滚事务重新开始读执行更新。

【定义】两段锁协议：

在对任何数据进行读、写操作之前，首先要获得对该数据的封锁；
在释放一个封锁之后，事务不再申请和获得任何其他锁。
两段锁协议是实现可串行化调度（多个事务的并发执行结果与按某一顺序的串行执行结果相同）的充分条件

【定义】锁的粒度：锁的作用范围，从高到低分为：数据库、表、记录、列，选择的时候要考虑并发度（其他事务能否访问）和开销（系统的资源占用），但实际上由数据库系统自动设置：

安全性控制

登录身份验证
使用用户账户
权限管理

备份

完全备份：备份整个数据库，需要较多的时间和空间
差异备份：进行一次完全备份后，只备份发生变化的那部分数据，其优点是备份的数据量较少，存储和还原的速度快
事物日志备份：事务日志是记录数据库变动的独立文件，每次备份只需复制自上次备份以来对数据库所作的改变。事务日志备份花费的时间较少。
文件：需指定一个文件或文件组的列表，仅对这些被指定的文件或文件组进行备份。

最后更新于 March 16, 2020

SCUTEEE 写作者指南v1.3 电子秤电路